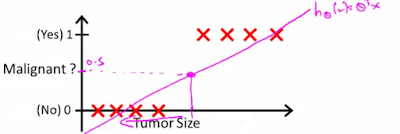
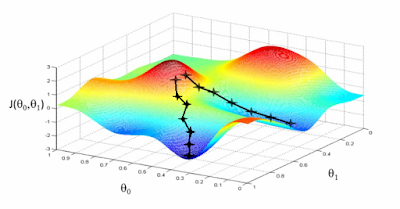
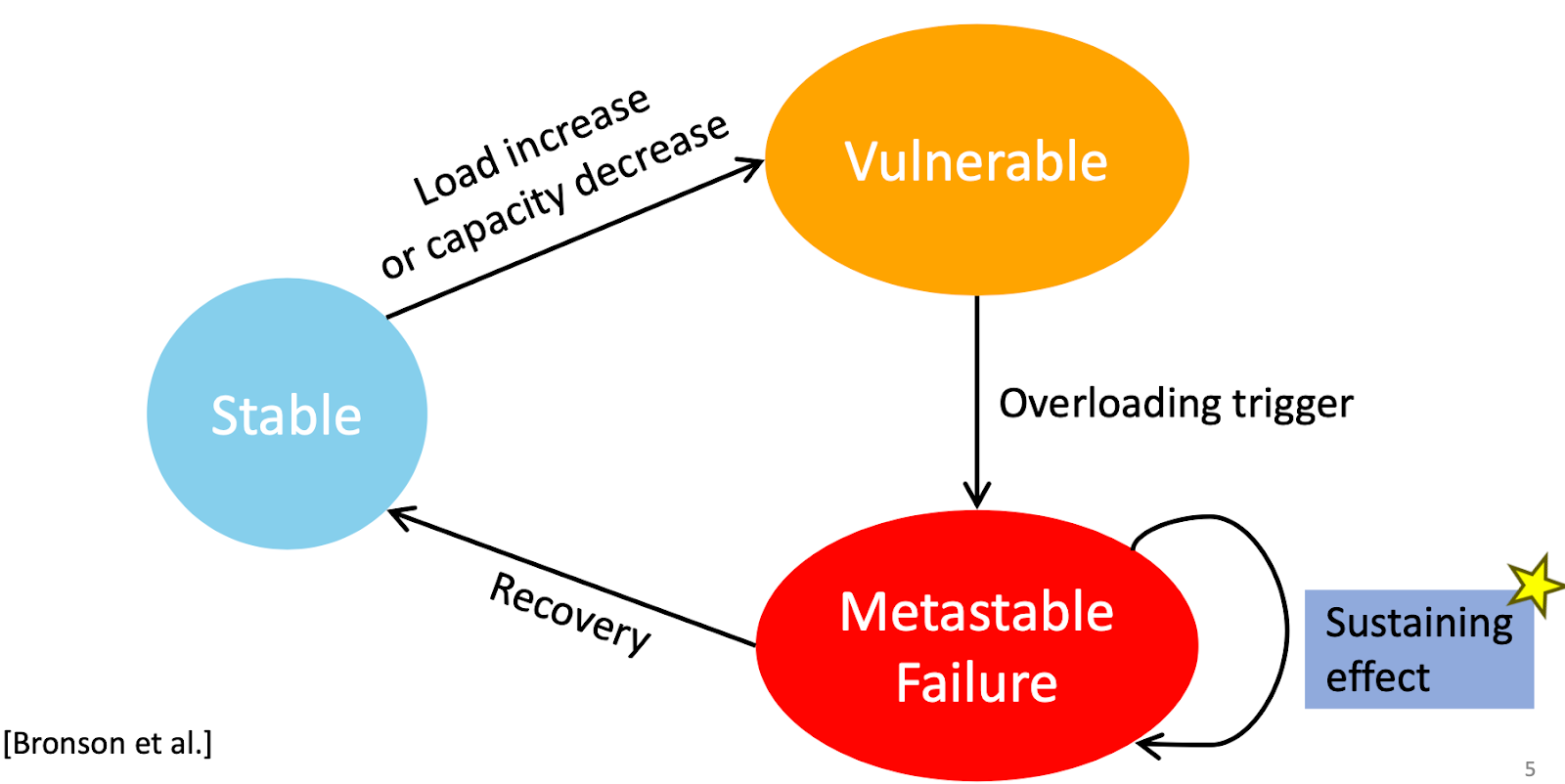
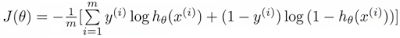Deep Learning With Dynamic Computation Graphs (ICLR 2017)
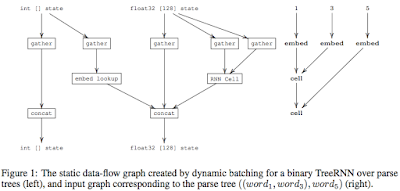
This is a paper by Google that is under submission to ICLR 2017. Here is the OpenReview link for the paper. The paper pdf as well as paper reviews are openly available there. What a concept! This paper was of interest to me because I wanted to learn about dynamic computation graphs. Unfortunately almost all machine learning/deep learning (ML/DL) frameworks operate on static computation graphs and can't handle dynamic computation graphs. (Dynet and Chainer are exceptions). Using dynamic computation graphs allows dealing with recurrent neural networks (RNNs) better, among other use cases. ( Here is a great article about RNNs and LSTMs . Another good writeup on RNNs is here .) TensorFlow already supports RNNs , but by adding padding to ensure that all input data are of the same size, i.e., the maximum size in the dataset/domain. Even then this support is good only for linear RNNs not good for treeRNNs which is suitable for more advanced natural language processing. This was a ve